Oogst overtollige energie
Hoe de overtollige energie in een off-grid situatie gebruikt kan worden
Bron: Hugh Piggott (homepower #179)
Mensen met zonnepanelen en windmolens die off-grid (zonder elektriciteitsnet) leven verafschuwen het om energie te verspillen. We houden ons bezig met efficiëntie, het uitdoen van het licht en energiezuinige laders. Maar we vergeten hoeveel energie er door de accu laad controllers niet gebruikt wordt. Dit artikel wil zicht geven op de mogelijkheden om dit overschot te benutten.
Windenergie wordt gegenereerd tijdens windrijke perioden net zoals zonne energie gegenereerd wordt tijdens de zonnige uren. Echter veel van de opgewekte energie wordt op een ander moment gebruikt bijvoorbeeld tijdens de avond of gedurende kalm weer. Hiervoor gebruiken we meestal accu's om de energie tijdelijk op te slaan totdat we deze nodig hebben.
Bronnen van hernieuwbare energie wekken de ene dag veel meer op dan de andere dag, afhankelijk van het weer en het seizoen. Er ontstaat een surplus als de accu de geleverde energie niet meer op kan slaan omdat de accu bijna 100% geladen is. De accu neemt naar gelang zijn laadtoestand steeds minder energie op. Deze manier van laden is ook noodzakelijk om de accu niet over te belasten en te zorgen dat deze zijn beoogde levensduur haalt. Maar dit resulteert vaak in ongebruikte energie. Het principe van laad controle regeling is het voltage optimaal te regelen naargelang de laad status van de accu. De installateur moet de laadregelaar voor ieder laad stadium (absorption, float, en equalize) van de juiste instellingen voorzien. In eerste instantie wordt de accu met een hoge stroom (amperes) geladen en deze wordt gedurende de tijd afgebouwd. De spanning (voltage) wordt redelijkerwijs constant gehouden. Een goede kwaliteit laadregelaar gebruikt ook de temperatuur van de accu voor het bepalen van de laadstroom en bepaald aan de hand van de tijd wanneer een accu zijn absorption stadium heeft doorlopen (geladen is). Hierna zal de accu met een lage stroom in het float stadium blijven.
Het principe van laad controle regeling is het voltage optimaal te regelen naargelang de laad status van de accu. De installateur moet de laadregelaar voor ieder laad stadium (absorption, float, en equalize) van de juiste instellingen voorzien. In eerste instantie wordt de accu met een hoge stroom (amperes) geladen en deze wordt gedurende de tijd afgebouwd. De spanning (voltage) wordt redelijkerwijs constant gehouden. Een goede kwaliteit laadregelaar gebruikt ook de temperatuur van de accu voor het bepalen van de laadstroom en bepaald aan de hand van de tijd wanneer een accu zijn absorption stadium heeft doorlopen (geladen is). Hierna zal de accu met een lage stroom in het float stadium blijven.
Een zonnepaneel laadregelaar limiteert de laadstroom naar de accu en beschermt deze tegen te snel laden zodat deze niet beschadigd wordt. De andere kant van het verhaal is dat hierdoor de efficiëntie van het systeem gereduceerd wordt omdat er minder energie gebruikt wordt dan aangeboden. Windenergie en hydro bronnen zijn niet zo eenvoudig onder controle te brengen. Als de turbine opbrengst niet gebruikt wordt kan deze door overbelasting (te hoog toerental) beschadigd worden. Om dit te voorkomen moet er een laadregelaar met overload controle (diversion controller) gebruikt worden. Deze schakelt overtollige stroom naar een dump-load zodat de accu beschermd wordt tegen overbelading en de wind(hydro) turbine toch belast blijft. De efficiëntie kan een stuk vergroot worden door nuttige dump-load's "opportunity diversion loads" te gebruiken in plaats van een dump-load die alleen de accu beschermd "protective diversion loads".
Dumpload beter benutten
 Normaliter zal de dump load van een windmolen installatie bestaan uit een aantal weerstanden die de ruimte verwarmen om er voor te zorgen dat de windmolen niet onbelast kan draaien als er geen net-koppeling is of als de accu’s opgeladen zijn. In veel gevallen betekent dit gewoon dumpen van overtollige energie. Om deze zogenaamde overtollige energie toch beter te benutten heeft Hugh Piggott een schakeling ontwikkeld die de dump load monitort en een zinnige belasting ingeschakeld als er stroom naar de dump load wordt gestuurd. Dit kan bijvoorbeeld een warm water boiler zijn.
Normaliter zal de dump load van een windmolen installatie bestaan uit een aantal weerstanden die de ruimte verwarmen om er voor te zorgen dat de windmolen niet onbelast kan draaien als er geen net-koppeling is of als de accu’s opgeladen zijn. In veel gevallen betekent dit gewoon dumpen van overtollige energie. Om deze zogenaamde overtollige energie toch beter te benutten heeft Hugh Piggott een schakeling ontwikkeld die de dump load monitort en een zinnige belasting ingeschakeld als er stroom naar de dump load wordt gestuurd. Dit kan bijvoorbeeld een warm water boiler zijn.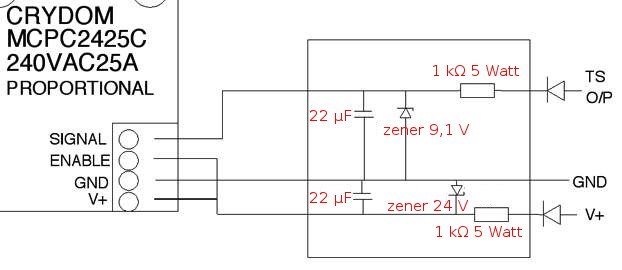
De schakeling is ontwikkeld op basis van een microprocessor gestuurde solid state relais (lastrelais voor gedeeltelijke sturing van het vermogen van een AC-lading). De functie van de dump load wordt niet aangetast dus de beveiliging van de windmolen blijft onveranderd.
In het schematische voorbeeld is uitgegaan van een 24 volt accu systeem met een Tristar controller. Op de website van scoraigwind vind je uitgebreide informatie en daar wordt ook een schakeling beschreven om meerdere zinnige belastingen in een reeks aan elkaar te koppelen.
Virya op basis van fietsonderdelen
Van de hand van Adriaan Kragten zijn weer een aantal handleidingen verschenen, een van de handleidingen is de uitwerking van een molen met een wiekdiameter van één meter op basis van een fietsnaaf en acht neodymium magneten.
 Dit is een variant op de Virya 1.04 die al eerder verschenen is en deze is op basis van een naaf-fietsdynamo.
Dit is een variant op de Virya 1.04 die al eerder verschenen is en deze is op basis van een naaf-fietsdynamo.
In de handleiding wordt gebruik gemaakt van aluminium om wieken van te maken, tevens zijn de tekeningen voor de buigmallen uitgewerkt. Het hele ontwerp is met berekeningen bewezen dus de bouwer kan rekenen op een maximaal vermogen van 6 watt bij 12 volt. De beveiling is meganisch door middel van een wegklappende staartvaan en zal er altijd voor zorgen dat het toerental binnen veilige grenzen blijft.
| Download | ||||||||
In this manual the 3-bladed VIRYA-1.04, electricity generating windmill, Drawings; In this manual the 3-bladed VIRYA-1.04, electricity generating windmill,
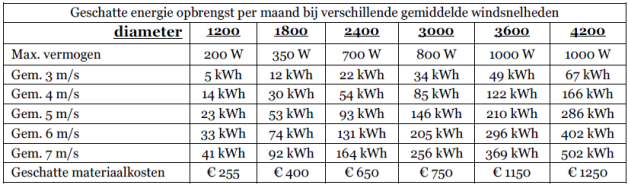
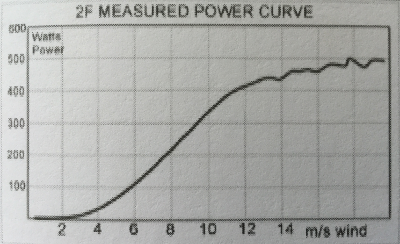
De beweging "windempowerment" die tot doel heeft om kennis te delen bij het bouwen ontwikkelen en onderhouden van locaal gebouwdewind molens heeft zijn website vernieuwd. Het ziet er nu nog duidelijker en overzichtelijker uit. De website is een bron van informatie voor de verdere ontwikkeling van de kleine zelfgebouwde windmolen. The present document is a maintenance manual for “Piggott“ based designed small wind turbines (SWT), developed by WindEmpowerment (WE) association (... ing. Adriaan Kragten stelt al zijn rapporten gratis ter beschikking hiermee komt een grote hoeveelheid kennis voor iedereen binnen handbereik. Adriaan is iemand met vele jaren ervaring in windenergie zijn activiteiten zijn zoals hij het zelf omschrijft: "Kragten Design is a one man engineering office founded in 1989 and directed by ing. (B.Sc.) Adriaan Kragten. The main activities of this business are the development of small electricity generating windmills with PM-generators, supplying of consultancy and the writing of technical reports. Building plans of eighteen wind turbines with rotor diameters between 1 and 4.6 metre are developed." Hieronder een overzicht van de specificaties. Er is een ruime keuze aan wiek diameter en verschillende type dynamo zoals omgebouwde a-synchroon motoren, vlakke plaat generator of een fiets naaf dynamo. . Samen met Joh Leary van de Sheffield universiteit zijn metingen verricht en is de onderstaande power curve diagram samengesteld. |




 Renewable energy world
Renewable energy world
 Watt is duurzaam
Watt is duurzaam





